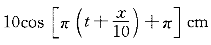己知t=0.5s的波形如图所示,波速大小u=10m/s,若此时P点处媒质元的振动动能在逐渐增大,则波动方程为( )。


正确答案:
B
答案解析:
【解析】由t=0.5s的波形曲线图(a)知:A=10cm,λ=20cm,ω=2πν=2π(u/λ)=2π(10/20)=π·s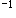 。
。
且此时P点质元的动能在增大,应向平衡位置靠近,下一时刻的波形曲线如图(b)中虚线所示。由此得出此波沿X负方向传播,进而得出当t=0.5s时坐标原点(x=0)的质元在平衡位置且向y轴的反向运动。
即:
ωt+φ=3π/2
故:
φ=3(π/2)-ωt=3(π/2)-π/2=π
波动方程为
y=10cos[π(t+x/10)+π]
所以选B。
【点评】根据波形图可以确定波长(λ),振幅(A)。根据某点P振动图可以确定周期(T)代入波速u=λ/T和角频率ω=2π/T,求出波速和角频率。根据P点质元的动能在增大,判断P点应向平衡位置靠近,判断出下一时刻的波形曲线如图(b)中虚线所示。再根据波形图的移动方向可以判断波的传播方向,得出此波沿x负方向传播。根据初始条件t=0时,初位移y=y ,初速度υ=υ
,初速度υ=υ 求解初相φ。运用选定系数法,设波动方程为y=Acos[ω(t-x/u)+φ],分别将求得振幅(A)、波速(u)、角频率ω、初相φ代入方程即可求解。
求解初相φ。运用选定系数法,设波动方程为y=Acos[ω(t-x/u)+φ],分别将求得振幅(A)、波速(u)、角频率ω、初相φ代入方程即可求解。
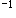 。
。且此时P点质元的动能在增大,应向平衡位置靠近,下一时刻的波形曲线如图(b)中虚线所示。由此得出此波沿X负方向传播,进而得出当t=0.5s时坐标原点(x=0)的质元在平衡位置且向y轴的反向运动。
即:
ωt+φ=3π/2
故:
φ=3(π/2)-ωt=3(π/2)-π/2=π
波动方程为
y=10cos[π(t+x/10)+π]
所以选B。
【点评】根据波形图可以确定波长(λ),振幅(A)。根据某点P振动图可以确定周期(T)代入波速u=λ/T和角频率ω=2π/T,求出波速和角频率。根据P点质元的动能在增大,判断P点应向平衡位置靠近,判断出下一时刻的波形曲线如图(b)中虚线所示。再根据波形图的移动方向可以判断波的传播方向,得出此波沿x负方向传播。根据初始条件t=0时,初位移y=y
 ,初速度υ=υ
,初速度υ=υ 求解初相φ。运用选定系数法,设波动方程为y=Acos[ω(t-x/u)+φ],分别将求得振幅(A)、波速(u)、角频率ω、初相φ代入方程即可求解。
求解初相φ。运用选定系数法,设波动方程为y=Acos[ω(t-x/u)+φ],分别将求得振幅(A)、波速(u)、角频率ω、初相φ代入方程即可求解。